프로젝트를 수행하다보면, Chart 를 사용하는 경우가 정말 많은것 같습니다.
수행하는 업무에 따라 사용하는 Chart 의 종류는 달라지겠지만, 대부분 Line 관련 Chart 는 많이 사용하는것 같습니다.
단순히 y = ax + b 와 같은 1차 함수를 사용한 Chart 도 있겠지만, 여러 points 를 line 으로 연결해서 표현하는 Chart 가
오히려 일반적일 것 같습니다. point to point 를 직선으로 연결하는 line chart 도 있지만, 포인트 들을 부드러운 곡선으로 구성되어 있는 Chart도 쉽게 찾아 볼 수 있습니다.
html canvas 자체 함수로 quadraticCurveTo 함수를 제공하고 있지만, 실제로는 베지에(Bezier) 곡선을 활용하는 것이라, 부드러운 곡선을 얻기는 하지만, 주어진 모든 점을 통과 하지는 않습니다.
각 구간별 모든 점을 통과 하면서, 부드러운 곡선을 그리기 위해서는 최소 2차 함수 이상이 각 구간별로 구성되어야 곡선을 구성할 수 있습니다.
2차 함수로 구성하는 것을 Qudratic Intepolation 이라 하고, 3차 함수로 연결하는 것을 Cubic Interpolation 이라고 합니다. 여러 포인트를 구간별로 연결하는 곡선은
그 구간별로 보간(Interpolation) 하여야 하기 때문에 각 구간은 다른 계수를 지닌 수식이 다른 함수 일텐데 어떻게 부드럽게 연결할 수 있는지 정리해 보고자 합니다.
3차 함수가 더 부드럽게 연결할 수 있으나 이해하기에는 2차 함수로 이해하는게 더 좋을 것 같아서 2차 함수를 중심으로 확인해 보겠습니다.
Spline 곡선
Spline을 위키의 정의 에는 복수의 포인트를 통과하는 부드러운 곡선이라고 이야기 하고 있습니다.
https://ko.wikipedia.org/wiki/%EC%8A%A4%ED%94%8C%EB%9D%BC%EC%9D%B8_%EA%B3%A1%EC%84%A0
여러 지점을 통과하고 구간별 함수가 2차 함수라면 단순하게 생각해서 다음과 같은 표현을 생각 할 수 있습니다. 함수 원형과 1차 미분 함수의 형태 입니다.
$$ y = ax^2 + bx + c \\ y^\prime = 2ax + b \\ $$
주어진 x,y 데이터(point)가 가르키는 점은 앞의 구간 함수와 뒤의 구간 함수가 교차하는 지점입니다. 해당 지점에서 두개의 함수는 같은 값을 반환할 수 있어야 합니다.
어떤 포인트 p0 에서 p1 으로 가는 구간의 함수 하나와 p1 ~ p2 로 가는 구간의 함수, 그외 주어진 포인트 n 개 까지의 구간 함수를 생각해 볼 수 있습니다.
우리가 구하고자 하는 함수의 갯수는 포인트의 갯수가 n 이라고 할 때 구간함수의 갯수는 n-1 개의 함수를 구해야 하는 것입니다.
예를 들어 point 가 p0, p1, p2, p3, p4 의 5개가 있다면 구하고자 하는 함수는 p0 ~ p1 까지의 S1, p1 ~ p2 까지의 S2, p2 ~ p3 까지의 S3, p3 ~ p4 까지의 S4 의 4개의 함수를 구해야 합니다.
이것을 간단히 정리하면 다음과 같습니다.
$$
points : p0, p1, p2, p3, p4 \\
p0 에서 p1 까지의 함수 \quad S1 = a_1x^2 + b_1x + c_1 \\
p1 에서 p2 까지의 함수 \quad S2 = a_2x^2 + b_2x + c_2 \\
p2 에서 p3 까지의 함수 \quad S3 = a_3x^2 + b_3x + c_3 \\
p3 에서 p4 까지의 함수 \quad S4 = a_4x^2 + b_4x + c_4 \\
$$
예시에서 5개의 points 가 있고, 구간이 4개니, 총 4개의 함수가 구간별로 필요합니다. 각 구간별 함수는 2차함수를 사용한다고 하였으니, 각 3개의 미지수가 존재합니다.
각 구간별 a, b, c 가 그에 해당하는 미지수 입니다. 총 12개의 미지수를 찾아야 하기 때문에 최소 12개의 다항식이 필요합니다.
실제로 포인트를 다음의 값으로 가정해 보겠습니다. p0 = {x: 0, y: 0}, p1 = {x: 100, y: 222}, p2 = {x: 200, y: 200}, p3 = {x: 300, y: 229}, p4 = {x: 400, y: 400} 이렇게 예시된 값으로 확인해 보도록 하겠습니다.
각 포인트 에서 값을 확인해 보겠습니다.
$$
\begin{aligned}
S1 = a_1 (p0.x)^2 + b_1 (p0.x) + c_1 = (p0.y) \quad a_1 (0)^2 + b_1 (0) + c_1 = (0) \\
S1 = a_1 (p1.x)^2 + b_1 (p1.x) + c_1 = (p1.y) \quad a_1 (100)^2 + b_1 (100) + c_1 = (222) \\
S2 = a_2 (p1.x)^2 + b_2 (p1.x) + c_2 = (p1.y) \quad a_2 (100)^2 + b_2 (100) + c_2 = (222) \\
S2 = a_2 (p2.x)^2 + b_2 (p2.x) + c_2 = (p2.y) \quad a_2 (200)^2 + b_2 (200) + c_2 = (200) \\
S3 = a_3 (p2.x)^2 + b_3 (p2.x) + c_3 = (p2.y) \quad a_3 (200)^2 + b_3 (200) + c_3 = (200) \\
S3 = a_3 (p3.x)^2 + b_3 (p3.x) + c_3 = (p3.y) \quad a_3 (300)^2 + b_3 (300) + c_3 = (229) \\
S4 = a_4 (p3.x)^2 + b_4 (p3.x) + c_4 = (p3.y) \quad a_4 (300)^2 + b_4 (300) + c_4 = (229) \\
S4 = a_4 (p4.x)^2 + b_4 (p4.x) + c_4 = (p4.y) \quad a_4 (400)^2 + b_4 (400) + c_4 = (400) \\
\end{aligned}
$$
구간 함수가 4개 있고, 시작점과 끝점에서의 값을 알기 때문에 각 함수당 2개의 수식을 만들 수 있습니다. 8개의 수식은 위의 예시처럼 만들어 볼 수 있었습니다.
곡선은 구간 함수(S1, S2, S3, S4) 접점에서 1차 미분값이 같습니다.
p1 점에서 S1 과 S2 의 곡선이 만나고 부드럽게 연결하기 위해서는 1차 미분값이 같아야 합니다. ( 직선의 기울기가 같음 )
p2 에서는 S2 와 S3 의 1차 미분이 같아야 하고, p3 에서는 S3 와 S4 의 1차 미분이 같아야 합니다.
$$
\begin{aligned}
S1 ^\prime = S2 ^\prime \quad 2 a_1 (p1.x) + b_1 = 2 a_2 (p1.x) + b_2 \quad 2 a_1 (100) + b_1 = 2 a_2 (100) + b_2 \\
S2 ^\prime = S3 ^\prime \quad 2 a_2 (p2.x) + b_2 = 2 a_3 (p2.x) + b_3 \quad 2 a_2 (200) + b_2 = 2 a_3 (200) + b_3 \\
S3 ^\prime = S4 ^\prime \quad 2 a_3 (p3.x) + b_3 = 2 a_4 (p3.x) + b_4 \quad 2 a_3 (300) + b_3 = 2 a_4 (300) + b_4 \\
\end{aligned}
$$
위의 식은 아래와 같이 표현할 수 있습니다.
$$
\begin{aligned}
S1 ^\prime - S2 ^\prime = 0 \quad 2 a_1 (p1.x) + b_1 - 2 a_2 (p1.x) - b_2 = 0 \quad 2 a_1 (100) + b_1 - 2 a_2 (100) - b_2 = 0\\
S2 ^\prime - S3 ^\prime = 0 \quad 2 a_2 (p2.x) + b_2 - 2 a_3 (p2.x) - b_3 = 0 \quad 2 a_2 (200) + b_2 - 2 a_3 (200) - b_3 = 0 \\
S3 ^\prime - S4 ^\prime = 0 \quad 2 a_3 (p3.x) + b_3 - 2 a_4 (p3.x) - b_4 = 0 \quad 2 a_3 (300) + b_3 - 2 a_4 (300) - b_4 = 0 \\
\end{aligned}
$$
첫번째 구간 함수는 2차 미분값이 0 입니다.
총 12개의 필요한 수식중 지금 3개를 찾았으니 마지막 하나만 정의 하면 해를 풀 수 있습니다.
마지막 하나는 시작점 함수의 2차 미분 값을 0으로 설정하는 것으로 단순하게 정의하고 있습니다.
$$
S1 ^{\prime\prime} = 2 a_1 = 0 \quad 단순하게적용 \quad a_1 = 0 \\
$$
값이 0이라 단순하게 적용해서 계산하고 있습니다.
이제 12 개의 수식이 나왔으니, 복잡하더라도 해를 구할 수 있습니다. ( 해가 있다면요 … )
$$
\begin{bmatrix}
0&0&1&0&0&0&0&0&0&0&0&0\\
10000&100&1&0&0&0&0&0&0&0&0&0\\
0&0&0&10000&100&1&0&0&0&0&0&0\\
0&0&0&40000&200&1&0&0&0&0&0&0\\
0&0&0&0&0&0&40000&200&1&0&0&0\\
0&0&0&0&0&0&90000&300&1&0&0&0\\
0&0&0&0&0&0&0&0&0&90000&300&1\\
0&0&0&0&0&0&0&0&0&160000&400&1\\
200&1&0&-200&-1&0&0&0&0&0&0&0\\
0&0&0&400&1&0&-400&-1&0&0&0&0\\
0&0&0&0&0&0&600&1&0&-600&-1&0\\
1&0&0&0&0&0&0&0&0&0&0&0\\
\end{bmatrix} \times
\begin{bmatrix}
a_1\\b_1\\c_1\\a_2\\b_2\\c_2\\a_3\\b_3\\c_3\\a_4\\b_4\\c_4\\
\end{bmatrix} =
\begin{bmatrix}
0\\222\\222\\200\\200\\229\\229\\400\\0\\0\\0\\0\\
\end{bmatrix}
$$
가우스 소거법을 이용하면 역함수를 구할 수 있듯이, 소거법을 활용하여 해를 구할 수 있습니다.
이렇게 구한 값입니다.
$$
\begin{aligned}
a_1 = 0, \quad b_1 = 2.22, \quad c_1 = 0 \\
a_2 = -0.0244 \quad b_2 = 7.1 \quad c_2 = -244.0007 \\
a_3 = 0.0295 \quad b_3 = -14.46 \quad c_3 = 1912.0031 \\
a_4 = -0.0153 \quad b_4 = 12.42 \quad c_4 = -2120.0061 \\
\end{aligned}
$$
위 수식을 이용하여 구간별로 곡선을 그려 보면 아래와 같은 그림이 그려집니다.
(구간의 범위는 x 값이 포함되는 영역에서 해당 구간 함수를 활용하면 됩니다. 에제에서 x 가 100 이면 S1 함수를 x 가 250 이면 S3 함수를 사용합니다.)
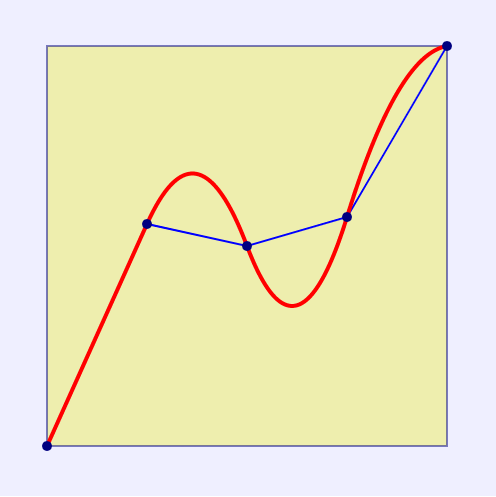
2차함수 이상을 구성하는 방법
처음 정리를 시작할 때는 2차함수기반 (Quaratic Spline Interpolation) 과 3차함수기반(Cubic Spline Interpolation ) 을 정리할 예정 이었습니다.
Cubic Spline 을 x 기반의 수식으로 구성할 경우 2차 함수를 구한 위의 방식을 약간만 수정하면 구할 수 있습니다. 미분을 1차 2차로 구성한 후,
처음과 끝의 2차 미분 함수의 값을 0 혹은 필요한 값으로 설정하는 것으로 계산을 진행할 수 있습니다.
x 값을 기반으로 하지 않고, t ( 0 ~ 1 ) 사이의 함수로 재구성하여 계산하는 방법은 한글로 된 사이트를 포함하여 많이 있기 때문에 참조한 사이트를
소개하는 것으로 갈음할까 합니다. 개인적으로는 위와 같은 x값 기반의 행렬을 구성해서 소거법을 활용하는 방식을 더 선호하는 편입니다.
Data 추세 등을 추정하는 함수를 구성할 때도 역행렬을 구성하는 방식으로 계수를 추출하는게 편하기 때문에 처음 계수를
계산할 때 드는 비용이 그렇게 문제가 될 만큼 크다고는 생각하지 않는 측면도 있습니다. 물론 지극히 개인적인 생각 입니다. ^^
참조 사이트
https://psu.pb.unizin.org/polynomialinterpretation/chapter/chapter-three-quadratic-spline-interpolation/
사실 이번에 정리하다 발견한 사이트 인데, 이 사이트를 보고는 자세히 정리하는 것을 포기(?) 하였습니다. 친절하게 하나씩 설명해 주는 사이트 입니다.
https://qt3b1s62da6s.tistory.com/416
Cubic Spline 을 설명한 사이트 입니다.
https://adnoctum.tistory.com/146
Cubic Spline 의 풀이를 소스로 구성해서 구성해 놓은 사이트 입니다.
https://mathworld.wolfram.com/CubicSpline.html
간결하지만 위 내용이 이해가 되면 정리하기 좋은 사이트 입니다.