Python - 개인적인 소감 …
Linux 에서 Shell 관련 프로그램을 개발해야할 필요성이 제기 되었을 때 Python 을 가능하지 않을까 하는
기대감에 이런 언어가 있구나 했던때가 2010년 경이 었던것 같습니다.
당시, 우리나라 개발환경의 주류가 java, c# 등이고, Ruby, Python 이 경쟁하고 있었고, 통계는 R, Linux 환경에서는
Shell Program 이 개인적으로 더 좋게 느껴졌던것 같습니다.
요즘 tensorflow.js 를 살펴보면서, AI 자료를 찾아 보면 대부분 Python 기반의 모듈이었습니다.
numpy, pandas, matplotlib 등의 모듈을 사용하면 계산, 분석, 시각화가 어렵지 않게 구현이 되면서도, 수행속도도 느리지 않습니다.
변수를 heap, stack, 전역 static 일지 고려한 코딩에서, 구현중심으로 변화하며, 즉각적인 확인이 필요한 영역에서 급격히 파급력을
높이는게 아닌가 합니다. tensorflow 관련 python 모듈을 찾아보다 보면, 개념만 이해하면, 구현이 복잡한 내용도 대부분 모듈화 되어 있어
편리한 사용이 가능한게 아닌가 합니다.
개념과 원리에 대한 학습이 충실하다면, 이런 모듈을 사용하는것이 생산성을 극대화 시킬 수 있을것 같은 생각이 들었습니다.
Python 시작
참조 URL
python 설치에 관련하여 많이 사용하는 모듈을 모두 함께 설치할 수 있는 anaconda 등이 있지만, 필요할 때 필요한 모듈을 설치해 놓고 사용하는 것이 학습을 위해서는 더 좋을 것 같습니다.
python 사이트에서 컴퓨터 OS 에 따라 프로그램을 다운 받아 진행하면 될 것 같습니다.
PYTHON URL : https://www.python.org/
Down load URL : https://www.python.org/downloads/release/python-3114/
Windows 설치시 가능하면 관리자권한의 모든사용자로 설치하는 것이 pip 으로 각 모듈을 설치할 때 편할것 같습니다. python 이 설치된 후 필요모듈을 설치하여야 하는데 이때 주의 하여야 할 부분이 관리자권한으로 설치하지 않으면 구성된 파일을 삭제 추가할 때 문제가 발생할 수 있기 때문에 cmd 창 혹은 visual studio code 를 실행할 때 관리자권한으로 뛰은 상태에서 pip 명령을 수행하시는게 좋습니다.
Numpy URL : https://numpy.org/install/
Pandas URL : https://pypi.org/project/pandas/
Matplotlib URL : https://pypi.org/project/matplotlib/
// python, pip version 확인
python --version
pip --version
// pip upgrade - 관리자모드 추천
python -m pip install --upgrade pip
python -m pip install -U pip
// 설치
pip install numpy
pip install pandas
// mapplotlib site 에서 제시하는 방법
python -m pip install -U pip
python -m pip install -U matplotlib
간단한 Python 모듈을 통해 다른 언어와 무엇이 비슷하고 무엇이 다른지를 확인해 보고자 합니다.
Python 은 주로 분석모듈에 많이 사용하기 때문에 numpy 와 matplotlib 을 활용하여 최소제곱법으로 구현된
간단한 회귀식을 구성해 보고자 합니다.
Python 과 비교할 언어는 Javascript 와 Java 입니다. 가급적 유사한 방식으로 구현해 보고자 다른 Library 는 제외 하였습니다.
최소제곱법 ( Least Square Method, Simple Linear Regression)
자료를 검색해 보면 한글로된 좋은 사이트도 많이 보이고 있습니다.
주어진 X,Y 값을 기준으로(2개 이상의 점) 추세를 예측할 수 있는 1차 함수를 구성하기 위한 방법으로 사용합니다.
최소제곱법은 오차 제곱의 합이 최소한이 되도록 구성하는 방법이며, 1차 이상의 함수에서도 적용할 수 있습니다. 이글에서는 1차 함수만 대상으로 하겠습니다.
구현을 위해서는 기본적인 공식이 필요하기 때문에 간단히 정리해 보겠습니다.
$$
\bar{y} = a \times \bar{x} + b \\
\bar{x} = xPoint 평균( meam ) \\
\bar{y} = yPoint 평균( mean ) \\
a = \frac{\sum\limits_{i=1}^n (({x_i} - \bar{x})\times({y_i} - \bar{y}))} { \sum\limits_{i=1}^n(({x_i}-\bar{x})^2)} \\
b = \bar{y} - a \times \bar{x}
$$
xPoint 가 1, 2, 3, 4, 5 이고 yPoint 가 3, 5, 7, 9, 11 일 경우 기울기가 2이고, 절편이 1 인 y = 2 * x + 1 인 수식을 예상할 수 있습니다.
이런 부분을 예측해 내기 위해 1차 최소제곱법을 사용하게 됩니다.
원리에 대한 설명은 네이버캐스트에 잘되어 있기 때문에 링크로만 연결하겠습니다.
한글 설명 URL : https://terms.naver.com/entry.naver?docId=3569970&cid=58944&categoryId=58970
Wiki URL : https://en.wikipedia.org/wiki/Least_squares
Python 으로 구성하기
Python 을 정리하기 위해서 구성하는 모듈이므로, 간단하게 구성해 보겠습니다.
import 구문으로 numpy, matplotlib.pyplot 을 가져오고 있습니다.
def 로 함수 구문을 구성하고 있는데, numpy 의 mean 함수가 평균을 구하는 함수라 굳이 makeMeanValues 라는 함수를 구성할 필요는 없으나, 다른 언어와 유사한 구조를 취하기 위해서 구성해 보았습니다.
기본값을 설정하는 방식이 slope=2.0 등으로 parameter 변수가 없을 경우 default 값을 설정할 수 있습니다. 함수중 makeLinePoints 는 기울기와 절편을 기준으로 points 를 반환해 주는 함수 입니다. slope 과 intercept 는 기울기와 절편이고, bias 는 각 포인트별 흔들리는 정도를 준것이라 보면 될것 같습니다.
makeSimpleLinearRegression 함수는 기본적인 validation 만 수행합니다. 실무에서라면 각 함수는 에러 핸들링이 필수 입니다.
평균을 구하고, 각 포인트에서 평균을 뺀후 위의 공식에 따라 기울기를 구하고, 그 기울기를 기준으로 절편을 구해 반환하는 함수 입니다.
return slope, intercept 는 return 이 두번 일어나는 것이 아닌, python 자료형의 튜플로( 불변의 배열) 묶어 반환하고 있습니다. 문자열의 format 은 두가지 방식으로 구성해 보고 있습니다.
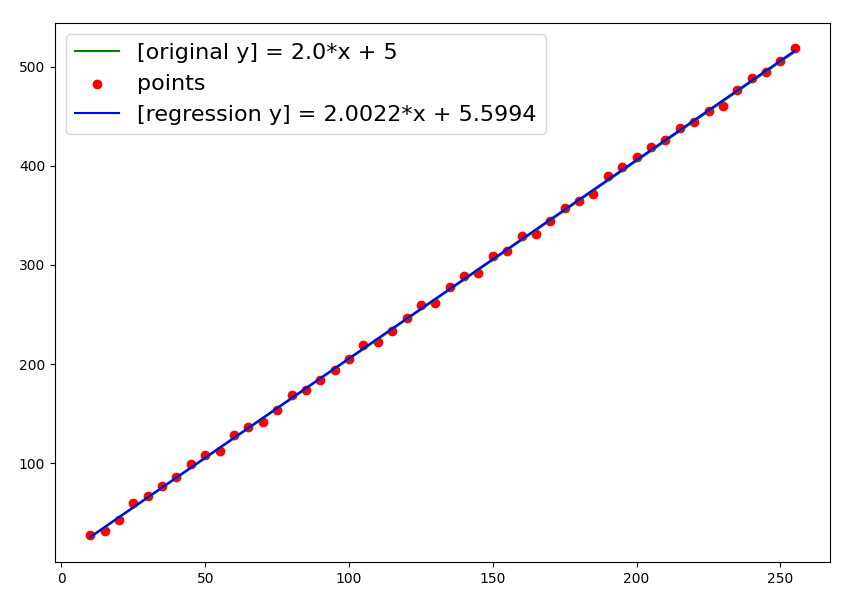
matplotlib.pyplot 으로 데이터를 chart 로 시각화 하여 표현하고 있습니다.
위의 내용을 구현한 코드는 아래와 같습니다.
import numpy as np
import matplotlib.pyplot as plt
def makeMeanValues(pointArray):
return np.mean(pointArray)
def makeLinePoints(size=50,slope=2.0,intercept=5,startX=5,xStep=1,bias=2.0):
xPoints = np.arange(startX, startX+xStep*size, xStep)
yPoints = xPoints*slope+intercept+bias*(np.random.rand(size)-0.5)*2
orgPoints = xPoints*slope+intercept
return xPoints, yPoints, orgPoints
def makeSimpleLinearRegression(xPoints,yPoints):
size = len(xPoints)
if ( size != len(yPoints)):
return
xAvg = makeMeanValues(xPoints)
yAvg = makeMeanValues(yPoints)
slope = ((xPoints-xAvg)*(yPoints-yAvg)).sum() / ((xPoints-xAvg)**2).sum()
intercept = yAvg - slope*xAvg
return slope, intercept
size = 50
slope = 2.0
intercept = 5
startX = 10
xStep = 5
bias = 5.0
xyPoints = makeLinePoints(size,slope, intercept, startX, xStep, bias)
calcResult = makeSimpleLinearRegression(xyPoints[0], xyPoints[1])
orgStr = "[original y] = {slope}*x + {intercept}".format(slope=slope,intercept=intercept)
calcStr = "[regression y] = %0.4f*x + %0.4f" % (calcResult[0], calcResult[1])
plt.figure(figsize=(10,7))
plt.plot(xyPoints[0], xyPoints[2], color='g', label=orgStr)
plt.scatter(xyPoints[0], xyPoints[1], color='r', label='points')
plt.plot(xyPoints[0],xyPoints[0]*calcResult[0]+calcResult[1], color='b', label=calcStr)
plt.legend(fontsize=16)
plt.show()
Javascript 로 구성하기
Python 과 유사한 구성으로 소스를 구성해 보았습니다.
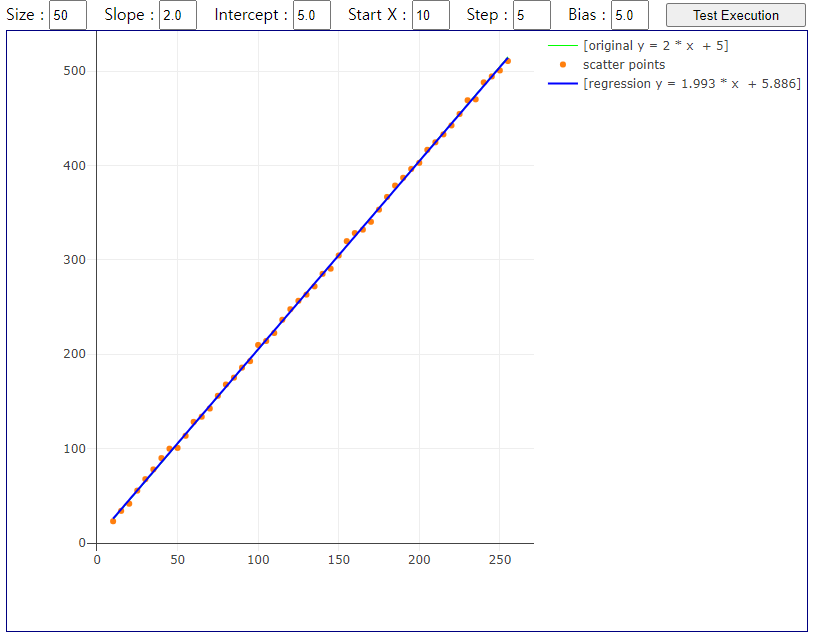
공통점을 부각시키기 위해서 함수도 map, reduce 등을 사용하였습니다. Chart 도 plotly.js 를 기준으로 구성하여 matplotlib 과 유사한 효과가 나타나도록 구성하였습니다.
다만, Web 이기 때문에 사용자가 데이터를 변경해서 확인해 볼 수 있도록 차트를 구성할 때 변수를 받아서 테스트 할 수 있도록 구성하였습니다.
이곳에서 적용된 예제를 확인할 수 있습니다.
<div>
Size : <input type="text" id="sizeTxt" value="50"/>
Slope : <input type="text" id="slopeTxt" value="2.0"/>
Intercept : <input type="text" id="interceptTxt" value="5.0"/>
Start X : <input type="text" id="startXTxt" value="10"/>
Step : <input type="text" id="stepXTxt" value="5"/>
Bias : <input type="text" id="biasTxt" value="5.0"/>
<BUTTON onClick="makeRegressionResult()">Test Execution</BUTTON>
</div>
<div style="width:800px;height:600px;border:1px solid #000080" id="chartDiv"></div>
<script>
const chartDiv = document.getElementById("chartDiv");
const makeMeanValues = (pointArray) => {
const sum = pointArray.reduce( (a,b) => a+b, 0.0);
return sum/pointArray.length;
};
const makeLinePoints = (size=50,slope=2.0,intercept=5,startX=5,xStep=1,bias=2.0) => {
const xPoints = [];
const yPoints = [];
const orgPoints = [];
for ( let i = 0; i < size; i++) {
let xv = startX+i*xStep;
let orgY = xv*slope + intercept;
let yv = orgY + ( (Math.random()-0.5)*bias*2);
xPoints.push(xv);
yPoints.push(yv);
orgPoints.push(orgY);
}
return [ xPoints, yPoints, orgPoints];
};
const makeSimpleLinearRegression = (xPoints,yPoints) => {
const size = xPoints.length;
if ( size != yPoints.length )
return;
const xAvg = makeMeanValues(xPoints);
const yAvg = makeMeanValues(yPoints);
const numerator = xPoints.map( (v,idx) => { return (v - xAvg) * (yPoints[idx] - yAvg); }).reduce( (a,b) => a+b, 0.0);
const denominator = xPoints.map( (v,idx) => { return (v - xAvg) * (v - xAvg); }).reduce( (a,b) => a+b, 0.0);
const slope = numerator/denominator;
const intercept = yAvg - slope*xAvg;
const calcPoints = xPoints.map(v => v*slope+intercept);
return [ slope, intercept, calcPoints];
};
const makeRegressionResult = () => {
const size = parseInt(document.getElementById("sizeTxt").value);
const slope = parseFloat(document.getElementById("slopeTxt").value);
const intercept = parseFloat(document.getElementById("interceptTxt").value);
const startX = parseFloat(document.getElementById("startXTxt").value);
const xStep = parseFloat(document.getElementById("stepXTxt").value);
const bias = parseFloat(document.getElementById("biasTxt").value);
const xyPoints = makeLinePoints(size,slope, intercept,startX, xStep, bias);
const sArray = makeSimpleLinearRegression(xyPoints[0], xyPoints[1]);
const orgName = "[original y = "+slope+" * x + "+intercept+"]";
const clalName = "[regression y = "+Math.round(sArray[0]*1000)/1000+" * x + "+Math.round(sArray[1]*1000)/1000+"]";
const orgPoints = {
x : xyPoints[0],
y : xyPoints[2],
type : 'scatter',
mode : 'lines',
line: {
color: '#00FF00',
width: 1
},
name : orgName,
};
const scatterPoints = {
x : xyPoints[0],
y : xyPoints[1],
type : 'scatter',
mode : 'markers',
color : 'red',
name : "scatter points",
};
const calcPoints = {
x : xyPoints[0],
y : sArray[2],
type : 'scatter',
mode : 'lines',
line: {
color: '#0000FF',
width: 2
},
name : clalName,
};
Plotly.newPlot(chartDiv, [
orgPoints,
scatterPoints,
calcPoints,
], {margin : {t :0 }});
};
makeRegressionResult();
</script>
open source 를 사용, 함수의 기본값 설정 등 상당히 유사한 문법 구조가 보입니다. 변수선언, 들여쓰기 문법등에서 차이가 있지만 유사한 점도 많아 보입니다.
Java 로 구성하기
언어별 공통점을 찾는 구성으로 Java 를 구현해 보았습니다.
차트까지 구성하려면 JavaFX 나 별도의 Library 를 사용하여야 하기 때문에 시각화는 추후 기회가 될 때 구성하고,
핵심적인 내용만 구성해 보았습니다.
거의 동일한 내용이라 소스만 비교할 수 있도록 기재해 보겠습니다.
import java.util.*;
import java.util.stream.*;
public class RegressionTest {
private double makeMeanValues( List<Double> pointArray ) {
if ( pointArray == null || pointArray.isEmpty() )
return Double.NaN;
double sum = pointArray.stream().reduce(0.0, Double::sum);
return sum/pointArray.size();
}
public List<List<Double>> makeLinePoints( int size, double slope, double intercept, double startX, double xStep, double bias) {
List<List<Double>> result = new ArrayList<List<Double>>();
List<Double> xPoints = new ArrayList<Double>();
List<Double> yPoints = new ArrayList<Double>();
List<Double> orgPoints = new ArrayList<Double>();
for ( int i = 0; i < size; i++ ) {
double xv = startX+i*xStep;
double orgY = xv*slope + intercept;
double yv = orgY + ( (Math.random()-0.5)*bias*2);
xPoints.add(xv);
yPoints.add(yv);
orgPoints.add(orgY);
}
result.add(xPoints);
result.add(yPoints);
result.add(orgPoints);
return result;
}
public List<Double> makeSimpleLinearRegression( List<Double> xPoints, List<Double> yPoints) {
int size = xPoints.size();
if ( size != yPoints.size() )
return null;
double xAvg = makeMeanValues(xPoints);
double yAvg = makeMeanValues(yPoints);
double numerator = IntStream.range(0,size).mapToDouble( i -> (xPoints.get(i) - xAvg) * (yPoints.get(i) - yAvg)).sum();
double denominator = IntStream.range(0,size).mapToDouble( i -> (xPoints.get(i) - xAvg) * (xPoints.get(i) - xAvg)).sum();
double slope = numerator/denominator;
double intercept = yAvg - slope*xAvg;
List<Double> result = new ArrayList<Double>();
result.add(slope);
result.add(intercept);
return result;
}
public static void main(String[] args) {
RegressionTest rObj = new RegressionTest();
int size = 50;
double slope = 2.0;
double intercept = 5.0;
double startX = 10.0;
double xStep = 5.0;
double bias = 5.0;
List<List<Double>> dataList = rObj.makeLinePoints(size,slope, intercept, startX,xStep, bias );
List<Double> sList = rObj.makeSimpleLinearRegression(dataList.get(0),dataList.get(1));
System.out.println ( sList );
}
}
정리
Python 에서 제공하는 내장 기능도 우수하지만, numpy , matplotlib 등 open source 로 제공되는 모듈은
개발에 필요한 중간 과정 이상의 함수를 구성해 놓은 것으로 보입니다.
개념만 이해하고 있다면, 구성해 놓은 모듈을 활용하여 상대적으로 귀찮은 작업없이 개발이 가능할 수 있다는 장점이 있는것 같습니다.
다만, 그 모듈을 구성한 사람 혹은 팀은 깊이있는 학습과 고민을 통해 모듈화를 진행하였을 것이기 때문에 사용하는 개발자가 그 원리를
확인하지 않고 사용만 한다면, 모듈에 종속될 가능성도 있어 보입니다.
언어별 차이점도 많지만, 근본적인 구성에서는 유사하지 않나 하는 생각을 해 보았습니다.